
minimum heap where the root is always the minimum value.ĭifference between PriorityQueue and TreeSet This is one point where you will see both similarities and differences between PriorityQueue and TreeSet in Java, like both, provide O(log(N)) complexity for adding, removing, and searching elements, but when you want to remove the highest or lowest priority element then PriorityQueue gives O(1) performance because it always keeps the element in the head, much like a heap data structure i.e. Similarly, TreeSet must re-arrange elements so that they remain the sorted order specified by Comparator or natural order imposed by Comparable.
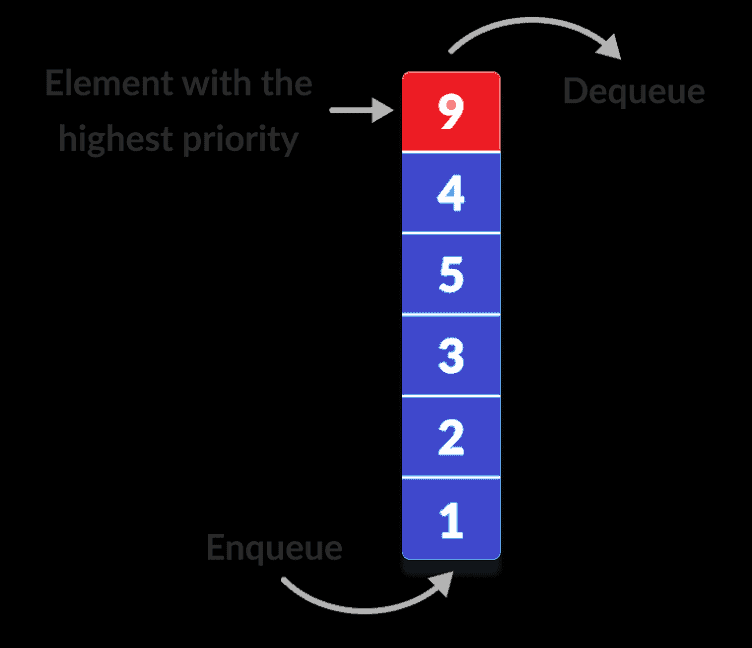
PriorityQueue must adjust after every insertion or deletion to keep the lowest or highest element in head position. When I say eligibility, which means which objects can be stored in PrioritySet and TreeSet? Is there any restriction or all objects are allowed? Well, there is, you can only store objects which implement Comparable or Comparator in both PriorityQueue and TreeSet because the collection classes are responsible for keeping their commitment i.e. This will help you to think of scenarios where you can use a PriorityQueue in place of TreeSet or vice-versa. What are similarities between PriorityQueue and TreeSetīefore looking at the difference between Priority Queue and TreeSet, let's first understand the similarities between them. You can use one in place of another in some scenarios but not in all scenarios and that's what the interviewer is looking for when he asked this question to you on Interview. This is one of the frequently asked Collection interview questions and what makes it interesting is the subtle difference between a lot of similarities between PriorityQueue and TreeSet. On the other hand, TreeSet keeps all elements in sorted order, and the iterator returned by TreeSet will allow you to access all elements in that sorted order. Only guarantee PriorityQueue gives that head will always be the smallest or largest element. It can contain multiple elements with equal values and in that case head of the queue will be arbitrarily chosen from them.Īnother key difference between TreeSet and PriorityQueue is iteration order, though you can access elements from the head in sorted order like head always give you lowest or highest priority element depending upon your Comparable or Comparator implementation iterator returned by PriorityQueue doesn't provide any ordering guarantee. both provide O(log(N)) time complexity for adding, removing, and searching elements, both are non-synchronized and you can get elements from both PriorityQueue and TreeSet in sorted order, but there is a fundamental difference between them, TreeSet is a Set and doesn't allow a duplicate element, while PriorityQueue is a queue and doesn't have such restriction. Space complexity of Dijkstra’s algorithm is O(V2) where V denotes the number of vertices (or nodes) in the graph.The PriorityQueue and TreeSet collection classes have a lot of similarities e.g. Time complexity of Dijkstra’s Algorithm Space complexity of Dijkstra’s algorithm
Best and Worst Cases for Dijkstra’s Algorithm The reason is, Fibonacci Heap takes O(1) time for decrease-key operation while Binary Heap takes O(Logn) time. Time complexity can be reduced to O(E + VLogV) using Fibonacci Heap.

#Priority queue time complexity code
So overall time complexity is O(E+V)*O(LogV) which is O((E+V)*LogV) = O(ELogV) Note that the above code uses Binary Heap for Priority Queue implementation. The inner loop has decreaseKey() operation which takes O(LogV) time.
If we take a closer look, we can observe that the statements in inner loop are executed O(V+E) times (similar to BFS). The time complexity of the given code/algorithm looks O(V^2) as there are two nested while loops. Dijkstra's Algorithm Running Time of Dijkstra’s algorithm


 0 kommentar(er)
0 kommentar(er)
